XII Edición

XIIª OLIMPIADA MATEMÁTICA COMUNIDAD DE MADRID
AÑO 2004

Organiza: S.M.P.M. Emma Castelnuovo
Colaboran: Centros de Apoyo al Profesorado

PROBLEMAS PROPUESTOS:

FASE SEMIFINAL

PRUEBA POR EQUIPOS

Problema 1: SUMA Y SIGUE
Fíjate bien en la siguiente suma.A B C DD C B AX X X X6 8 9 7Averigua los números que se esconden tras estas letras para que el resultado final de la suma sea efectivamente 6897.Para ello ten en cuenta las siguientes indicaciones:1.ABCD es un número formado por cuatro cifras consecutivas en orden creciente.2.DCBA es un número formado por las mismas cifras que las anteriores pero colocadas en orden inverso.3.XXXX es un número formado por las mismas cuatro cifras pero en orden desconocido.

Problema 2: LA ESCAMACalcular el área de la siguiente figura. Para ello, tomad sobre ella las medidas que necesitéis.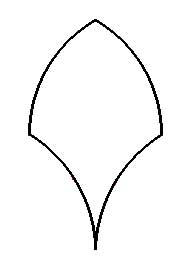

Problema 3: NÚMEROS CURIOSOSToma un número cualquiera de tres cifras, en general . Construye ahora otro de seis cifras repitiendo el primero dos veces consecutivas, es decir . Divide ahora el número que hayas obtenido entre 13, 11, y 7 sucesivamente. ¿Qué número obtienes? NOTA: Investiga para justificar porqué se obtiene este resultado.

Problema 4: TANGRAMComo sabes, una de las piezas del Tangram es un cuadrado. Supongamos que, tal y como indica la siguiente figura, su lado mide 2 cm. Determina a partir de este dato la longitud de los lados del resto de las piezas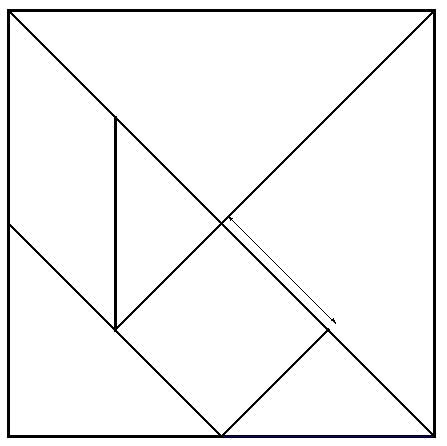

Recoge tus resultados sobre las siguientes figuras.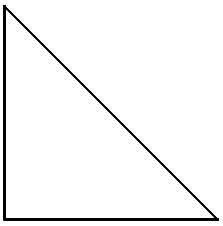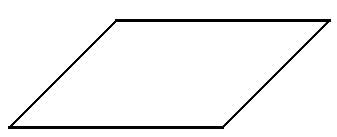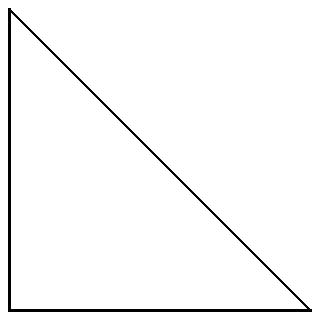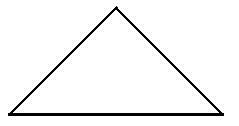

PRUEBA INDIVIDUAL

Problema 1: SUMAS EN FORMA DE MONTAÑALas siguientes filas representan la suma de una serie de números. En cada fila, el número más alto es el que está en el medio.11 + 2 + 11 + 2 + 3 + 2 + 11 + 2 + 3 + 4 + 3 + 2 + 11 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 11 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1¿Cuál será la suma de la serie en la que el número más alto es n?

Problema 2: RECUBRIENDO SUPERFICIES¿Podrían recubrirse las 63 casillas blancas de este tablero utilizando únicamente L – triminós?

Si es que sí, dibuja la solución encontrada. Si no, justifica su imposibilidad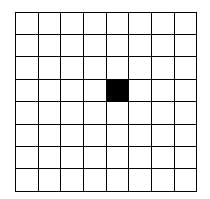

Problema 3: COMPONIENDO CANTIDADESForma tres números que cumplan las siguientes condiciones:1.- Cada número ha de tener tres cifras.2.- Debes utilizar las cifras del 1 al 9 sin que se repitan.3.- El segundo número ha de ser el doble que el primero y el tercero el triple que el primero.NOTA: Este problema tiene más de una solución, busca al menos dos soluciones.

Problema 4: CIRCUNFERENCIAS RODANDOTenemos tres circunferencias iguales de radio 2 centímetros que se están tocando tal y como indica la figura. Si hacemos rodar las circunferencias A y B apoyándose en la circunferencia C; a la misma velocidad, sin despegarlas y sin deslizarlas, ¿sabrías decir la distancia que ha recorrido el centro de la circunferencia A hasta que las dos circunferencias vuelvan a tocarse? ¿Y si solamente se moviera la circunferencia A, qué distancia recorrería ahora su centro? :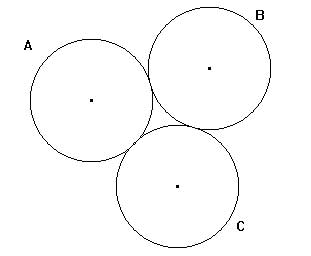

FASE FINAL

PRUEBA POR EQUIPOS

Problema 1: EL NÚMERO MISTERIOSOFormad un número con las cifras 1, 2, 3, 4, 5, 6, 7, 8 y 9, utilizando una vez cada una, de manera que las dos primeras cifras formen un número divisible por 2, las tres primeras formen un número divisible por 3 y así sucesivamente hasta el final.

Problema 2: LAS BOLASVíctor y Alicia intercambian bolas de colores. Una bola blanca la cambian por “x”bolas azules y una bola azul por “x”bolas rojas. Víctor tenía 2 bolas blancas, 4 azules y 3 rojas.
Al cambiarlas todas a rojas obtiene un total de 73 bolas rojas. Teniendo esto en cuenta, responded a las siguientes preguntas:
1.- ¿Cuál es valor de “x”?2.- ¿1 blanca por cuántas rojas se cambia?3.- ¿1 azul por cuántas rojas se cambia?

Problema 3: LA GUERRA DE LOS BARCOSEste problema se basa en el conocido juego de los barcos. Como sabes, cada jugador debe esconder en su tablero una flota compuesta de diez barcos que ocupan 1, 2, 3 ó 4 cuadrados contiguos situados horizontal o verticalmente, pero no en diagonal. La flota está formada por un barco de cuatro casillas, dos de tres casillas, tres de dos casillas y cuatro barcos de una casilla. Los barcos no se tocan entre si, ni siquiera en diagonal de manera que las casillas que rodean a cada uno de los barcos no pueden estar ocupadas por ninguno otro. Vuestro objetivo es localizar la posición de la flota enemiga sobre el tablero que os damos a continuación. Para ello tendréis que utilizar los números colocados a la derecha y debajo de cada tablero. Cada número indica la cantidad de casillas ocupadas por barcos en la fila o columna correspondiente. Para ayudaros, algunas casillas ya están marcadas.
NOTA: La figura siguiente muestra los barcos que tenéis que localizar y el significado de las casillas marcadas en el tablero.
Flota enemiga Casilla marcada sobre el tablero

Extremo de un barco (que sigue por el lado recto).

Agua (es aconsejable que lo utilices)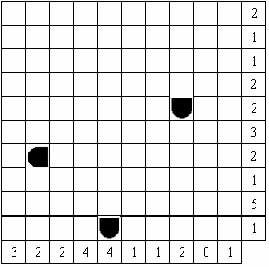

Problema 4: PAREJAS DE BAILEEn su pasada fiesta de cumpleaños, Lola invitó a 17 amigos. A cada uno de ellos le dio a la entrada una tarjeta con un número desde el 2 hasta el 18, reservándose el 1 para ella misma. Cuando todo el mundo estaba bailando se dio cuenta de que la suma de los números da cada pareja era un cuadrado perfecto. Teniendo esto en cuenta, descubrid cuál es el número de la pareja de Lola.

PRUEBA INDIVIDUAL

Problema 1: ¿DONDE COLOCAMOS LOS NÚMEROS?Estudia y describe de la manera más detallada posible el criterio de agrupamiento que se sigue en cada una de las columnas.
ABCDE 12348765 910111213141516 18192021———— ———————— Una vez que has hecho lo anterior, di en que columna colocarías los siguientes números. 100 , 327 , 3650 , 1019 , 448

Problema 2: JUEGA CON CUBOSImagina que sobre una hoja como la que representa la figura que tienes debajo y en la que hemos escrito en cada una de sus cuatro esquinas las letras A, B, C y D, construimos un cuerpo geométrico con cubos del modo y en la cantidad que indica el dibujo.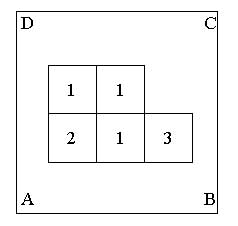

Los siguientes dibujos muestran el cuerpo geométrico que tendrías que construir, visto desde cada una de las cuatro esquinas de la hoja. Debajo de cada dibujo, pon la esquina desde la que se está viendo.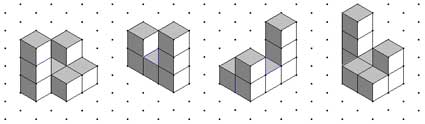

Esquina ……Esquina ……Esquina ……Esquina ……Imagina ahora que construyeses con cubos el cuerpo geométrico que te indica el siguiente dibujo.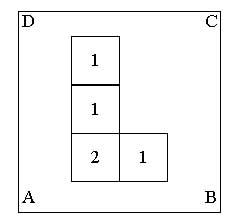

Dibuja sobre la siguiente trama isométrica cómo se vería desde cada esquina e indica de qué esquina se trata.

Problema 3: EL HELIPUERTO

Un helipuerto de forma cuadrada, tiene una hectárea de superficie y posee cuatro potentes focos de luz situados en los vértices del recinto. Por necesidades del tráfico aéreo se desea duplicar su superficie pero sin variar su forma y además, debido al modo en el que está hecha la instalación eléctrica, los focos deben permanecer en el mismo lugar y sobre el perímetro del helipuerto.
Haz un dibujo que ilustre la manera en la que construirías el helipuerto. Describe con la mayor exactitud posible, el lugar donde quedarán situados los focos en el nuevo helipuerto.

Problema 4: &AacuteNGULOS RECTOS

Determina cuál es el número máximo de ángulos rectos que puede tener un polígono de n lados, considerando tanto los ángulos interiores como los ángulos exteriores. Comienza analizando el caso de los polígonos de tres lados, de cuatro lados, de cinco lados etc. y trata de generalizar los resultados que obtienes.

MEJORES CLASIFICADOS

Entradas recientes

Comentarios recientes