| XIIIª OLIMPIADA MATEMÁTICA COMUNIDAD DE MADRID AÑO 2005 |
| Organiza: S.M.P.M. Emma Castelnuovo Colaboran: Centros de Apoyo al Profesorado |
CONVOCATORIA
Con el fin de promover la enseñanza y el aprendizaje de las Matemáticas a través de la resolución de problemas y del trabajo en equipo, se convocó la «X Olimpíada Matemática para el alumnado de 2º de ESO de la Comunidad de Madrid», organizada por la Sociedad Madrileña de Profesores de Matemáticas «Emma Castelnuovo», con la colaboración de los Centros de Apoyo al Profesorado de la Comunidad de Madrid, y cuya fase final tuvo lugar el pasado sábado 30 de Mayo, en las instalaciones del C.R.I.F. «Las Acacias».
Las bases de esta convocatoria de la Olimpiada así como la ficha de Inscripición han sido envíados a socios y Centros de Apoyo al Profesorado para su distribución entre los interesados en participar.
| PROBLEMAS PROPUESTOS: |
| FASE SEMIFINAL |
 PRUEBA POR EQUIPOS |
Problema 1: EL TRAPECIOCuatro hermanos heredan una finca como la que tienes en la figura. Evidentemente quieren repartírsela en partes iguales pero además tienen el capricho de que las cuatro partes tengan la misma forma. |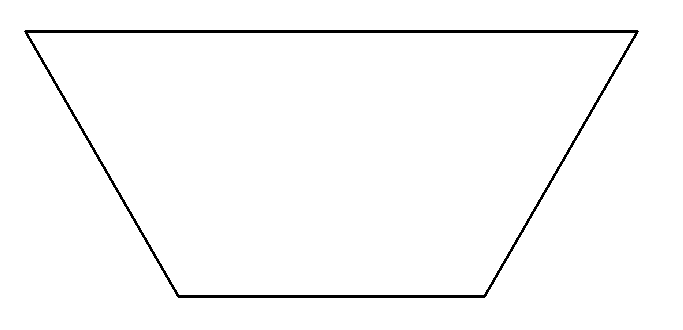
| ¿Seríais capaces de indicar cómo tendrán que hacerlo? |
| Problema 2: EL D.N.I.Se me ha olvidado el número de mi carné de identidad, pero tenía escrita esta clave por si lo perdía.Tiene ocho cifras.El número es el mismo leyéndolo en orden inverso, es decir, de delante hacia atrás o de atrás hacia delante.La cuarta cifra es la mitad de tres veces la primera.La tercera es igual a dos veces la primera, más la segunda.La tercera más la segunda suman doce.El doble de la primera, más cinco, es nueve.¿Podríais decirme cuál es el número de mi carné de identidad? |
| Problema 3: EL HOMBRE Y EL PERROUn hombre está paseando a su perro en dirección a su casa a una velocidad constante de 4 km/h. Cuando están a 10 km de casa el hombre suelta el perro y este corre inmediatamente hacia casa a 6 km/h. Cuando el perro llega a casa vuelve a correr a la misma velocidad hacia el hombre. Cuando lo alcanza vuelve a dirigirse a la casa. Esto se repite hasta que el hombre llega a casa y deja entrar al perro. ¿Cuántos kilómetros recorre el perro desde que lo suelta hasta entra en la casa? |
| Problema 4: CONSTRUYENDO BLOQUES CON CUBOSObservad cómo se van formando las siguientes figuras:Recoged los datos ordenadamente en una tabla y tratad de obtener la expresión que os permita averiguar la cantidad de cubos que tendría una figura en la que el número de plantas fuese uno cualquiera, “n”. Ayudándoos de lo anterior, ¿cuántos cubos se necesitarían para formar una figura siguiendo el patrón de las anteriores pero con 50 plantas?  |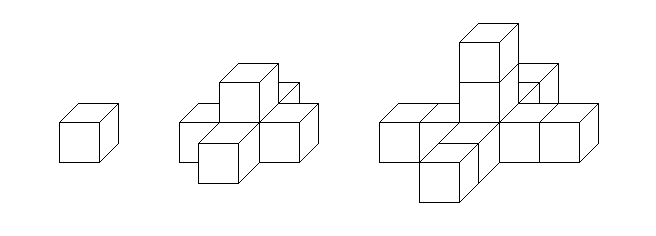
| PRUEBA INDIVIDUAL |
Problema 1: PANAL DE DECIMALES |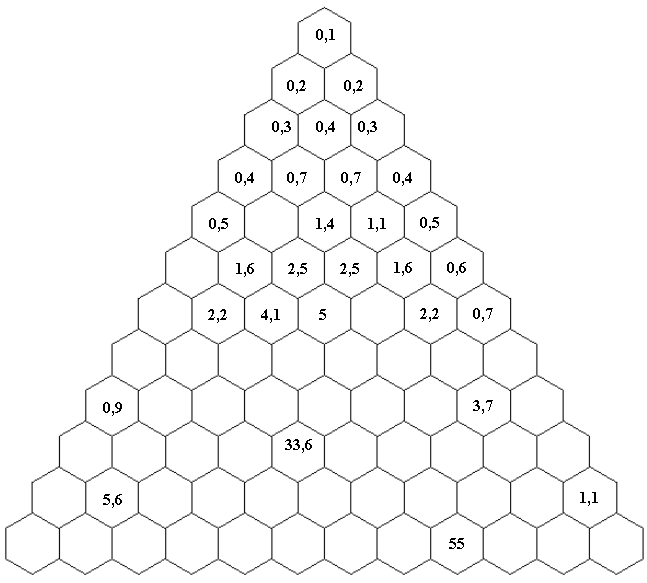
Problema 2: RELLENA EL CUADRADOConsiderando lados de 1, 2, 3, 4, 5, 6, 7, 8, 9 y 10 centímetros, sin repetir ninguno y usándolos todos, puedes formar cinco rectángulos cuyas áreas midan 9 cm², 16 cm², 18 cm², 28 cm² y 50 cm², de modo que con ellos puedas construir el cuadrado de la figura, que tiene 11 centímetros de lado. |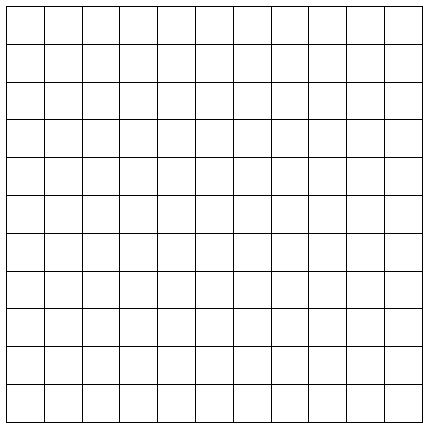
Problema 3: POLIMINÓSLlamamos “Poliminós” a todos aquellos polígonos que sobre una trama de puntos ortogonal como la que tienes más abajo, pueden formarse uniendo cuadrados, por los lados.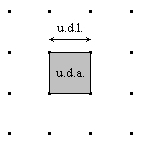 Tomando como unidad de área (u.d.a.) la del cuadrado más pequeño que puede formarse sobre la trama de puntos y como unidad de longitud (u.d.l.) el lado de dicho cuadrado, dibuja todos los poliminós que puedas que tengan como perímetro 12 unidades.NOTA1: Consideraremos Poliminós iguales todas aquellos que puedan superponerse aplicándoles un movimiento cualquiera, es decir, una traslación un giro o dándoles la vuelta (reflexión)Calcula además el área de todos los poliminós que construyas. ¿Qué conclusiones puedes sacar de tu estudio?  NOTA2: A continuación, tienes otra trama de puntos para que hagas tus razonamientos. |
Problema 4: NÚMEROS PERDIDOSCada una de las siguientes tres tiras contienen tres números. Todas ellas están formadas siguiendo la misma regla. Como puedes observar, las tiras están incompletas. Trata de descubrir la regla que se sigue para formarlas y escribe los números que faltan. |
| FASE FINAL |
| PRUEBA POR EQUIPOS |
| Problema 1: CADA UNO CON SU PAREJAEn una fiesta se ha reunido una pandilla formada por la misma cantidad de chicos que de chicas, de manera que se disponen a bailar en parejas. Nos gustaría que descubrieseis cómo se han formado las parejas.De cada una de ellas, evidentemente, tenéis que averiguar el nombre de la chica y del chico. También queremos saber la edad de cada uno de ellos, la posición que ocupa según la estatura cada chico y el color del pañuelo que lleva puesto cada pareja y que les diferencia de las demás.Para ello os ofrecemos los siguientes datos: Las edades de las chicas suman 110 años.La mayor tiene 29 años y es especialista en maratones de rock.Paco tiene cuatro años más que su pareja de baile. Es el más joven de los chicos y tiene 30 años.Alberto se lleva dos años con su pareja Y es el más alto.Clara tiene 27 años.Las edades de los cuatro chicos suman 126 años.Rosa y Alberto son pareja. El chico que baila con Nuria, que además lleva el pañuelo de color lila, se lleva tantos años con ella como Clara con su pareja. tiene dos años menos que Rosa que es la Que baila con el color rojo.Carlos, que es el más bajo, no baila con Clara.Juan es una año menor que Carlos, lleva el color verde y es un poco más bajo que Alberto.Merche ha llegado tarde y no tiene tiempo de cambiarse de ropa para el maratón, pero se ha puesto el pañuelo de color azul. |
Problema 2: CUADRADO MÁGICO DEL SALTO DEL CABALLO.Como podéis observar, el tablero que os mostramos a continuación tiene forma de cuadrado. En cada una de las casillas tenemos escrita una expresión algebraica. Lo que tenéis que hacer es averiguar el valor de todas y cada una de las incógnitas que aparecen. Para ello el dato que os damos es que en este tablero, todas las líneas horizontales y verticales suman 260.Una vez que hayáis descubierto el valor de cada una de las incógnitas, si obtenéis el valor numérico de las expresiones algebraicas de cada casilla, podéis comprobar que partiendo del número 1, los siguientes números naturales; 2, 3, 4, 5…… van apareciendo si sobre el tablero nos movemos siguiendo el movimiento del caballo en el juego del ajedrez. |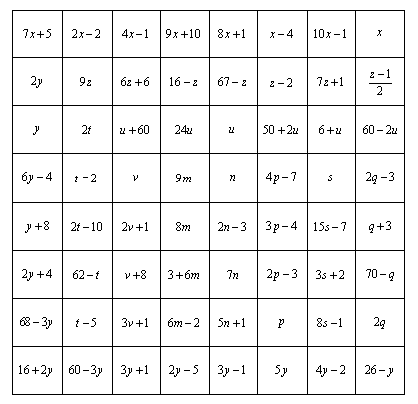
Problema 3: PUNTOS EN EL CUADRADOObservad las siguientes figuras, en ellas se muestra como en cada una vamos construyendo un cuadrado mayor sobre una trama ortogonal, dejando inscritos en él todos los anteriores.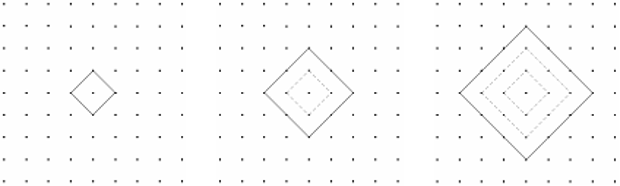 Primero cuadradoSegundo CuadradoTercer CuadradoAnalizad cuidadosamente cada una de ellas, tomad nota en cada caso de la cantidad de puntos que hay en el perímetro del cuadrado construido y de la cantidad de puntos que quedan en el interior de dicho cuadrado.A partir de los datos que habéis obtenido, descubrid la expresión que nos permitiría conocer en un caso cualquiera, la cantidad de puntos que tendríamos tanto sobre el perímetro del cuadrado como en su interior.Aplicad la expresión que habéis obtenido para indicar la cantidad de puntos que tendríamos sobre el perímetro y el interior del vigésimo cuadrado que construyéramos siguiendo este proceso de formación. |
Problema 4: MOSAICOCalcula el área de una de las baldosas que forman esta composición, sabiendo que el segmento mide 6 cm. y el segmento mide 5,2 cm. |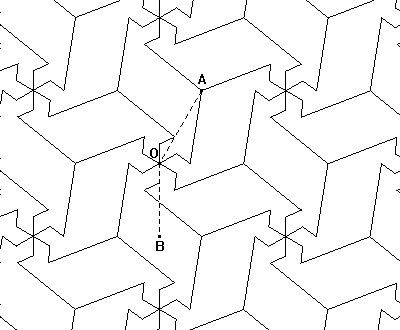
| PRUEBA INDIVIDUAL |
| Problema 1: PIEZAS ENCAJABLESImagina que construimos con cubos dos piezas como las que tienes en la figura. |
 |
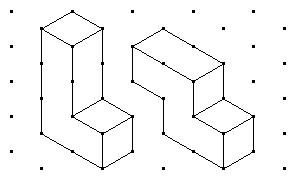| Tal y como se te muestra en el siguiente ejemplo, estas dos piezas pueden unirse apropiadamente para construir distintas figuras. |
 |
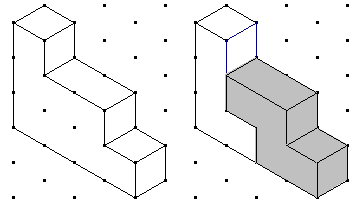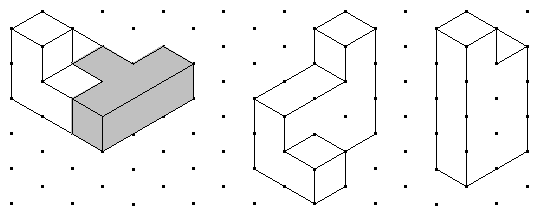
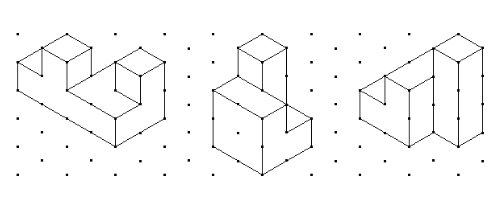
Utilizando las mismas dos piezas trata de imaginar cómo deberías unirlas para formar las siguientes figuras y sombrea sobre el dibujo una de las dos piezas para indicar cómo lo has hecho. |
  |
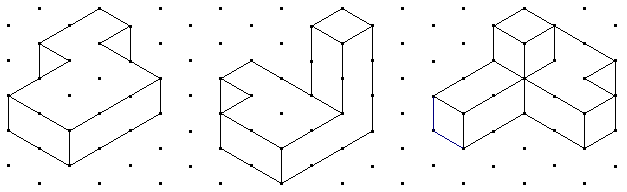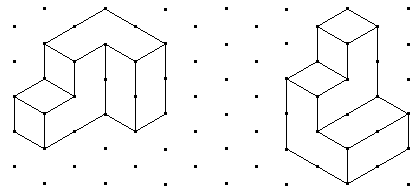| Haz lo mismo ahora con las siguientes dos piezas y las figuras que te damos a continuación. |
 |
 |
 |
| Problema 2: TARJETAS DE NAVIDADLas pasadas Navidades, en mi clase todas las chicas y chicos intercambiamos entre nosotros y con la profesora tarjetas de Navidad. En total se intercambiaron 900 tarjetas.Serías capaz de descubrir cuántos chicos y chicas hay en mi clase, sin contar a la profesora, teniendo en cuenta que:La cantidad de chicas es el doble que la de chicos.Cada chica dio una tarjeta a cada una de las otras chicas, a cada chico y a la profesora.Cada chico también dio una tarjeta a cada uno de los otros chicos, a cada chica y a la profesora.La profesora no dio ninguna tarjeta, pero colgó una felicitación en el tablero del aula deseándonos a todos una feliz Navidad e insistiendo en que trabajáramos más el próximo año. |
Problema 2: SUMA DE FRACCIONESComo puedes observar, a continuación te presentamos una serie formada por la suma de sucesivas fracciones en las que los denominadores siguen una regla que te será fácil descubrir.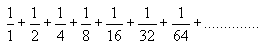 Ve obteniendo los resultados al ir sumando los dos primeros términos, los tres primeros términos y así sucesivamente, para a partir de ellos descubrir la expresión que nos permitiría conocer la suma de una cantidad cualquiera “n” de términosUtiliza esa expresión para obtener el resultado de sumar los veinte primeros términos de esta serie. |
GANADORES
Los resultados fueron los siguientes:
| MEJORES CLASIFICADOS |
Estos son los diez alumnos mejor clasificados en la Fase Final de la Olimpiada Matemática de la Comunidad de Madrid. Los tres primeros son los representantes de la Comunidad de Madrid en la Fase Nacional de la XIV Olimpiada Matemática Nacional organizada por la Sociedad Riojana de Profesores de Matemáticas «A prima», siendo ésta una de las actividades que se engloba dentro del programa de actividades de la Federación Española de Profesores de Matemáticas.