| XV OLIMPIADA MATEMÁTICA COMUNIDAD DE MADRID AÑO 2007 |
| Organiza: S.M.P.M. Emma Castelnuovo Colaboran: Centros de Apoyo al Profesorado |
CONVOCATORIA
Con el fin de promover la enseñanza y el aprendizaje de las Matemáticas a través de la resolución de problemas y del trabajo en equipo, se convocó la «X Olimpíada Matemática para el alumnado de 2º de ESO de la Comunidad de Madrid», organizada por la Sociedad Madrileña de Profesores de Matemáticas «Emma Castelnuovo», con la colaboración de los Centros de Apoyo al Profesorado de la Comunidad de Madrid, y cuya fase final tuvo lugar el pasado sábado 26 de Mayo, en las instalaciones del C.R.I.F. «Las Acacias».
Las bases de esta convocatoria de la Olimpiada así como la ficha de Inscripición han sido envíados a socios y Centros de Apoyo al Profesorado para su distribución entre los interesados en participar.
| PROBLEMAS PROPUESTOS: |
| FASE FINAL |
| Problema 1: BESOS Y ABRAZOSLos Gómez y los López se encuentran por la calle, rápidamente se produce un efusivo intercambio de besos y abrazos. Cada uno de los López saluda a cada uno de los Gómez. Al saludarse dos varones se dan un abrazo, mientras que al saludarse dos mujeres, o un hombre y una mujer, se dan un beso. Al final de la efusiva salutación se han producido 35 abrazos y 42 besos. ¿Cuántas mujeres y cuantos varones hay en cada familia? |
| Problema 2: UNO DE LOS EXÁMENESTres estudiantes, Antonio, Berta y Carlos, participan en una serie de exámenes. En cada prueba, el que queda primero recibe x puntos, el segundo recibe y puntos y el tercero z puntos, donde x, y, z son números enteros mayores que cero tales que x >y>z. No hay empates. En total, Antonio acumuló 20 puntos, Berta 10 puntos y Carlos 9 puntos. Antonio quedó el segundo en el examen de Álgebra.¿Quién quedó segundo en el examen de geometría? |
| Problema 3: LA PIRÁMIDE DE BOLASColocamos 15 discos según el diagrama de la figura.Sabiendo que el perímetro de cada disco es de 6 cms, a) ¿qué longitud tiene el perímetro exterior de esta figura? b) ¿qué longitud tendría el perímetro si la base de la figura estuviese formada por 6 discos? c) ¿y si la base estuviese formada por “n” discos? 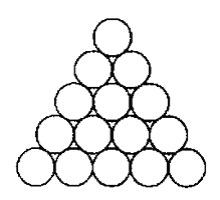 |
| Problema 4: LA BARRILESColocamos 15 discos según el diagrama de la figura.Sabiendo que el perímetro de cada disco es de 6 cms, a) ¿qué longitud tiene el perímetro exterior de esta figura? b) ¿qué longitud tendría el perímetro si la base de la figura estuviese formada por 6 discos? c) ¿y si la base estuviese formada por “n” discos?  |
| Problema 1: LOS NÚMEROS PRIMOSCuatro números primos se escriben de la siguiente manera: AA; BAB; BACD; AAAC Sabiendo que cada letra representa una cifra y que letras iguales corresponden a cifras iguales, ¿cuáles son esos números? |
Problema 2: EN EL LABERINTOSe quiere construir un laberinto en un jardín plantando a distancias iguales árbo-les para formar un seto en espiral, tal como indica la figura.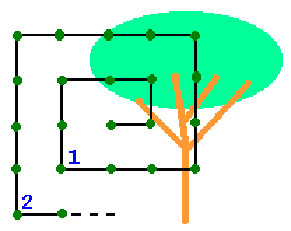 ¿Cuántos árboles deberán plantarse para que el laberinto sea de 10 vueltas? |
Problema 3: LA SOMBRAEn la figura, cada lado del cuadrado mide 1 dm. ¿Cuál es el área de la región sombreada?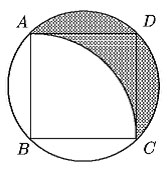 |
GANADORES
Los resultados fueron los siguientes:
| Alumno/a | Centro |
| Juan Martinez Olondo | C. Sta. Mª del Pilar |
| José Manuel Menéndez Encina | C. Sta. Mª del Pilar |
| Pedro Soria Postigo | C. Virgen Atocha |
Estos alumnos son los representantes de la Comunidad de Madrid en la Fase Nacional de la XVIII Olimpiada Matemática Nacional organizada por la Sociedad Navarra de Profesores de Matemáticas, siendo ésta una de las que se engloba dentro del programa de actividades de la Federación Española de Profesores de Matemáticas.
FINALISTAS
| Alumno/a | Centro |
| Belén Palomo Guerra | C. Sta Mª Pilar |
| Víctor Algora Jiménez | C. Sta Mª Pilar |
| Alberto González Fernández | JOYFE |
| Marina Bazarra Requena | C. Sta Mª Pilar |
| Lucia Murcia Tarancón | JOYFE |
| Belén Fernández Fernández | C. Fuentelarreyna |
| Inés Díez Martínez | Patrocinio de San José |
