| XVI OLIMPIADA MATEMÁTICA COMUNIDAD DE MADRID AÑO 2008 |
| Organiza: S.M.P.M. Emma Castelnuovo Colaboran: Centros de Apoyo al Profesorado |
Con el fin de promover la enseñanza y el aprendizaje de las Matemáticas a través de la resolución de problemas y del trabajo en equipo, se convocó la «XVI Olimpíada Matemática para el alumnado de 2º de ESO de la Comunidad de Madrid», organizada por la Sociedad Madrileña de Profesores de Matemáticas «Emma Castelnuovo», con la colaboración de los Centros de Apoyo al Profesorado de la Comunidad de Madrid.
Las bases de esta convocatoria de la Olimpiada así como la ficha de Inscripición han sido envíados a socios y Centros de Apoyo al Profesorado para su distribución entre los interesados en participar.
| PROBLEMAS PROPUESTOS: |
| FASE FINAL |
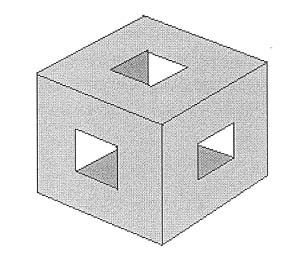
| Problema 1: EL CUBO GRUYÉREUn cubo de 3 por 3 tiene tres agujeros, cada uno con una sección de 1 por 1, que van desde el centro de cada cara en dirección a la cara opuesta, hasta que se encuentra y se une con otro agujero. ¿Cuál será la superficie total, en unidades cuadradas, del sólido que resulta? |
 |
Problema 2: BALANZAS Si una jarra pesa igual que una botella y un vaso. Una botella pesa lo mismo que un plato y un vaso. Dos jarras pesan lo mismo que tres  ¿Cuántos vasos pesarán lo mismo que una botella? |
Problema 3: PICOS CAÓTICOSObservamos los lados y picos de las siguientes figuras. La primera tiene 3 lados y 3 picos, la segunda tiene 12 lados y 6 picos, la tercera tiene 48 lados y 18 picos. Si continuamos el proceso ¿Cuántos picos tendrá la quinta figura? |
Problema 4: EL APARCAMIENTOEn un pequeño aparcamiento subterráneo los coches están aparcados como si fueran sardinas. Tan apretados están que solo pueden moverse para atrás y para delante. El coche número 1 de la figura, pertenece al director de una importante empresa y ¡tiene mucha prisa en salir!. Ayuda al encargado a encontrar el número mínimo de coches que deben ser movidos para que este señor pueda salir cuanto antes del atasco.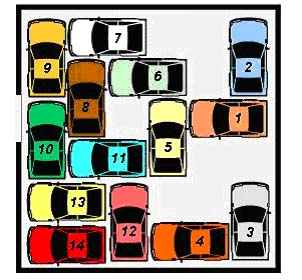 |
Problema 1: BANDERA NUEVAUn equipo de fútbol ha encargado su bandera bicolor a un prestigioso diseñador. Éste realizó el boceto a partir de un rectángulo en el que dividió cada lado en tres segmentos de la misma longitud; uniendo los puntos obtenidos como se indica en la figura. ¿En qué proporción se encuentran los colores que tiene que utilizar para la confección de la bandera?.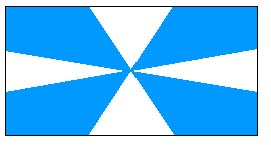 |
Problema 2: EL DÍA DEL CALENDARIOHemos cortado un cuadrado de tres días por tres días de la hoja de un calendario. Si la suma de las nueve fechas que contiene, es divisible entre 10 y además sabemos que la fecha de la esquina superior izquierda es múltiplo de 4. ¿Cuál es la fecha de la esquina inferior derecha? |
Problema 3: PUZZLE ALFABETICOOrdena estas piezas en un cuadrado 5×5, de forma que queden las mismas letras de arriba abajo que de izquierda a derecha. Es decir que las letras de una determinada fila sean las mismas que las de la correspondiente columna.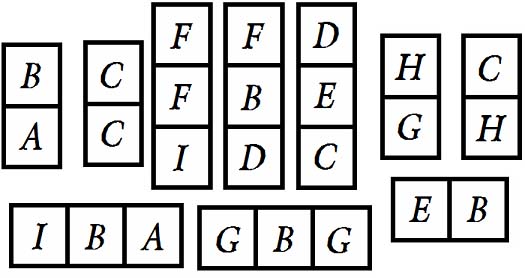 |
GANADORES
Los resultados fueron los siguientes:
| Alumno/a | Centro |
| Ciriano Cervantes, Enrique | Juan de la Cierva |
| Guerra Bernardo, Daniel | IES Gregorio Marañón |
| Pérez Iglesias, Adrián | IES Humanes |
Estos alumnos son los representantes de la Comunidad de Madrid en la Fase Nacional de la XIX Olimpiada Matemática Nacional organizada por la Sociedad de Profesores de Matemáticas de Murcia, siendo ésta una de las que se engloba dentro del programa de actividades de la Federación Española de Profesores de Matemáticas.
FINALISTAS
| Alumno/a | Centro |
| Navas Jiménez, Miguel Ángel | Gamo Diana |
| Redondo Castilla, Daniel | IES María Zambrano |
| Cobos Figueroa, Álvaro | IES Alameda de Osuna |
| Vallejo Luengo, Ernesto Pablo | C. Virgen Atocha |
| Sierra Sánchez, Julio César | Juan de la Cierva |
| Rico Caballero, Ignacio | IES Humanes |
| Reinoso Oytero, María | Patrocinio de San José |
