RESULTADOS DE LA FASE FINAL XVIII OLIMPIADA MATEMATICA
Estos alumnos son los representantes de la Comunidad de Madrid en la Fase Nacional de la XXI Olimpiada Matemática Nacional organizada por la Sociedad de Profesores de Matemáticas de Baleares, siendo ésta una de las que se engloba dentro del programa de actividades de la Federación Española de Profesores de Matemáticas (FESPM) y este año tendrá lugar del 24 al 28 de junio en las islas Baleares.
Ganadores:
| Alumno/a | Centro |
| Adrián Navarro Hernández | Joyfe |
| Velia Del Milagro Benites Piscoya | IES Severo Ochoa |
| Laura Pascual Fernández | IES San Fernando |
Finalistas:
| Alumno/a | Centro |
| Pablo Ojeda Higera | Joyfe |
| Sergio Ruiz Rico | IES Las Lagunas |
| David Dong Wu | IES Ágora |
| Miguel Luengo Escacena | Colegio Santa María del Pilar |
| Raúl Suarez Millán | IES Dámaso Alonso |
| Adrian Pérez González | IES Alpedrete |
| Daniel Herrero Saboya | IES San Fernando |
RESULTADOS DE LA GYMKHANA
A lo largo de la tarde, de forma complementaria y con un carácter más lúdico, nuestros participantes disfrutaron de una Gymkhana en los jardines de la finca Vista Alegre.
El grupo ganador de la Gymkhana fue: __
_____ _____, formado por los siguientes alumnos:
| Alumno/a | Centro |
| Jinle Xia | IES Ágora |
| Julia García Pérez | Colegio Cardenal Spínola |
| Oscar Villa | IES Jaime Ferrán |
| Noelia Martinez Lozano | IES Dámaso Alonso |
| María Andrés Tejedor | IES Isaac Albéniz |
| Sergio Ruiz Rico | IES Las Lagunas |
Un año más queremos felicitar a todos estos chic@s que con tanto entusiasmo participan en esta Olimpiada y dar las gracias a todos aquellos compañeros que comparten con nosotros objetivos como la enseñanza y aprendizaje de las matemáticas a través de la resolución de problemas y que con su participación hacen posible la celebración de esta Olimpiada.
PROBLEMAS DE LA FASE FINAL XVIII OLIMPIADA MATEMÁTICA
La Fase Final de la XVIII Olimpiada Matemática de la Comunidad de Madrid, se desarrolló el 29 de mayo en el CRIF Las Acacias, ubicado dentro del recinto conocido como Finca de Vista Alegre.
Los 54 alumn@s clasificados para esta fase tuvieron que resolver tres problemas individualmente y otros cuatro en grupo.
Problemas que tuvieron que resolver individualmente:
TIJERAS ABIERTAS
| ¿Qué distancia hay entre las puntas de unas tijeras que forman un ángulo de 60º, si las hojas de las tijeras miden 15 cm? |  |
| COLOR Y FIGURA Sobre la mesa hemos colocado estas 16 cartas. ¿Cuántas cartas, cuáles de ellas y porqué debemos dar la vuelta, para averiguar si cada carta roja tiene una figura al otro lado? |  |
| LOS AFILADORES Herrero, hojalatero, afilador,…nos parecen profesiones del pasado, próximas algunas de ellas a la extinción. Hace algunos años, dos amigos afiladores con escasos medios económicos decidieron comprar entre los dos una piedra de afilar. |  | |
 Acordaron que uno de ellos utilizase la piedra hasta que el tamaño de ésta se hubiera reducido a la mitad, y luego se la daría al otro. La piedra tenía un diámetro de 1 metro, con un orificio de 10cm en el centro, como muestra la imagen. ¿Cuál sería el diámetro de la piedra al recibirla el segundo amigo? | ||
Problemas que tuvieron que resolver en grupo:
CAMINO DEL COLE
Ana, en su camino diario al colegio, ha comprobado que si va a andando a 4km/h llega 5 minutos tarde, pero si se da prisa y va a 5km/h llega 10 minutos antes de la hora. ¿Cuál es la distancia al colegio? ¿Llegará puntual si hace la mitad del camino a 4km/h y la otra mitad a 5km/h?
| PULSANDO TECLAS Inicialmente hay un 1 en la pantalla. Al apretar la tecla A se multiplica por 3 el número de la pantalla. Al apretar la tecla B, se resta 1 al número de la pantalla. Utilizando una secuencia de teclas A y B hay que llegar a tener en la pantalla el 97. ¿Cuál es el número mínimo de teclas que se deben usar? |  |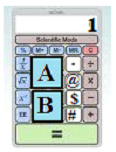
TRIÁNGULOS CON NÚMEROS
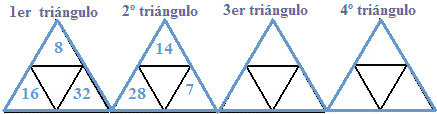
Siguiendo el orden lógico de estos dos triángulos, completa el tercero y el cuarto.
MEJOR COMPARTIR
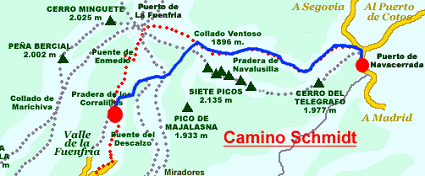
El último fin de semana Luis estuvo en la sierra haciendo el Camino Schmidt. Esta senda supone entre 6 y 7 horas de marcha. A media mañana se encontró con otros dos excursionistas que llevaban 15 y 9 barritas energéticas respectivamente para reponer fuerzas durante todo el día. Le invitaron no sólo a unirse a ellos en la senda, sino también a compartir sus barritas energéticas.
Luis, que es muy agradecido, les dio los 8€ que llevaba en el bolsillo. ¿Cuál es el reparto más justo de ese dinero entre los dos excursionistas?
ALUMNOS CLASIFICADOS PARA LA FASE FINAL DE LA XVIII OLIMPIADA
En primer lugar damos las gracias a todos los alumnos y profesores que participaron en la fase semifinal y felicitamos a los que se han clasificado para la siguiente fase.
ALUMNOS CLASIFICADOS PARA LA FASE FINAL
DE LA XVIII OLIMPIADA MATEMÁTICA
| IES Ágora | David Dong WuAndrea Zamora JiménezJinle Xia | |
| IES Alameda de Osuna | Guillermo Escanciano FernándezCarmen Martínez JiménezJavier Vidiella García | |
| IES Alpedrete | Carlos Mondejar PedrazaAdrian Pérez GonzálezMiguel Angel Rivas Pozo | |
| Colegio Cardenal Spínola | Belén López ÁlvarezJulia García PérezAlejandro Navarro Motllo | |
| IES Dámaso Alonso | Isabel Marín RayoNoelia Martinez LozanoRaúl Suarez Millán | |
| IES Isaac Albéniz | María Andrés TejedorLara Gómez ChilenoManuel Aranda Díaz | |
| IES Jaime Ferrán | Ester GarcíaLucas de la TorreOscar Villa | |
| Joyfe | Claudia Gil IrazabalPablo Ojeda HigeraAdrián Navarro Hernández | |
| IES Las Lagunas | Ana Caballero CastillejoSergio Ruiz RicoSergio Eiras | |
| IES León Felipe | Wei LiuDavid Morillo ValdiviaCarla Nieva Vallejo | |
| IES Leonardo Da Vinci | Julia Lozano MartínPaula Jiménez SáezPablo Rodríguez Delgado | |
| IES Miguel Catalán | Paula González MoncadaHugo Granda PérezJorge López-Tofiño | |
| IES Rey Pastor | Víctor Marín GonzálezHéctor Martín SerranoSilvia Maturana Álamo | |
| Salesianos Atocha | Valentina Anatolieva FisinskhaAndrei VilcuLucia Blanco Ortega | |
| IES San Fernando | Daniel Herrero SaboyaLaura Pascual Fernández Jaime López Navarro | |
| Colegio San Viator | Pablo Zapata RodríguezLidiya MakarovaJesús Salinas Pérez | |
| Colegio Sta María del Pilar | Antonio Rodríguez-YniestoSara Gancedo LesmesMiguel Luengo Escacena | |
| IES Severo Ochoa | Velia Del Milagro Benites PiscoyaDavid Nevado CatalánJavier Rojo Muñoz | |
La Fase Final se celebrará el próximo sábado 22 de mayo, en el CRIF “Las Acacias”, C/General Ricardos nº 179, metro de Oporto.
La fase final consiste en un día de convivencia entre chicos y chicas de distintos lugares de la Comunidad. Por la mañana se realizarán, a partir de las 10:00h, las pruebas por equipos e individuales. Por la tarde, tras la celebración de una Gymkhana Matemática, entre las 18:00 y 18:30, tendrá lugar la entrega de premios y diplomas de participación, con asistencia libre de familiares.
Este año 2010 la Final Nacional de las Olimpiadas se celebrará en Palma (Mallorca) y a ella asistirán los tres ganadores de esta fase final.
¡Suerte para todos los participantes!
Fase Semifinal XVIII Olimpiada Matemática
El miércoles 24 de marzo tuvo lugar la Fase Semifinal de la XVIII Olimpiada Matemática, participando en ella 67 Centros Educativos de nuestra Comunidad. Los alumn@s tuvieron que resolver cuatro problemas individualmente y otros cuatro en grupo.
Problemas propuestos para su resolución individualmente:
PARTES IGUALES Y DIFERENTES
El siguiente tablero es un cuadrado de 4×4. Juan quiere dividirlo en cuatro partes iguales manteniendo los cuadraditos enteros. Su amigo Luis le dice que él conoce varias formas de hacerlo y cada una de ellas con una figura diferente.
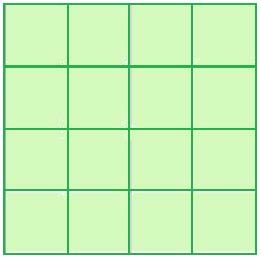
Ayuda a Juan y encuentra todas las diferentes figuras que permiten dividir el tablero en cuatro partes iguales.
CONTRATO LABORAL
Un repartidor de pizza a domicilio firma un contrato para la temporada de verano (12 semanas) por la que se le pagará con la motocicleta que necesita para el reparto más 1000 euros.
Tras 7 semanas el chico decide abandonar el trabajo para preparar los exámenes de septiembre. Por el tiempo trabajado la empresa le da la motocicleta y 200 euros.
EL CUADRADO INSCRITO
El cuadrado naranja está inscrito en el rojo de manera que corta cada lado del cuadrado grande en dos segmentos de 5cm y 3cm. ¿Cuál será el área del cuadrado naranja?
PEREGRINO EN EL CAMINO
Un peregrino es un viajero que visita algún lugar sagrado, casi siempre por motivos religiosos, siendo costumbre la visita de algunas de las iglesias que encuentra en el camino.
Nuestro peregrino decide, en la primera iglesia que entra, que si el santo le duplica el dinero que lleva en el bolsillo donará 200€. Al salir de la iglesia se produce el milagro y el peregrino cumple su promesa.
Al llegar a una segunda iglesia hace la misma promesa: donar 200€ si el santo le duplica el dinero que lleva en el bolsillo. De nuevo se produce el milagro y el peregrino cumple su promesa.
¿Cuánto dinero tenía el peregrino al inicio del camino, si al visitar la tercera iglesia realiza la misma promesa, el milagro se produce y el peregrino al cumplir su promesa se queda sin dinero?
Problemas propuestos para su resolución en grupo:
LA EDAD DE MI ABUELO
Mi abuelo siempre fue muy aficionado a las matemáticas, pero poco aficionado a decir su edad. Cansado de que se la preguntase (lo mismo que yo estaba cansado de preguntársela sin obtener respuesta), finalmente me dijo: “la suma de las cifras de mi edad es el doble de lo que valdrá la suma de las cifras de mi edad el año que viene“.
¿Cuántos años tiene?
CUIDADO CON LOS ROMANOS
Las siguientes operaciones con números romanos son correctas:
X · X = C
LIX + LVI = CXV
Sustituye cada letra por una cifra de forma que las operaciones resultantes sean también correctas. (Letras distintas corresponden a cifras distintas).
¿QUÉ HORA ES?
Esta mañana me he quedado dormido, en el recibidor del Instituto los tres relojes que hay marcan las siguientes horas:
La conserje me dice que uno hace veinte minutos que se ha parado, otro reloj está atrasado y otro de los relojes adelanta diez minutos. ¿Puedes ayudarnos a descubrir qué hora es? .
EN TIEMPOS DE CRISIS
Estas vacaciones, Carlos que vive en Madrid, alquiló un coche para ir hasta Barcelona y pasar un fin de semana con sus amigos. A mitad de camino, en Zaragoza, recoge a Pedro y a Laura. Una vez disfrutado el fin de semana, regresan juntos, Laura hasta Zaragoza y Pedro y Carlos continúan hasta Madrid.
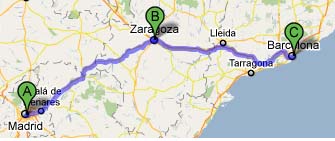
Como son buenos amigos, y estamos en tiempos de crisis, deciden repartir el gasto de la gasolina de forma equitativa.
Si el coste total asciende a 96€, ¿cuánto dinero debe poner cada uno de ellos? .
De esta fase, 18 grupos se clasificarán para pasar a la Fase Final que se celebrará el sábado día 22 de mayo.