PROBLEMAS DE LA FASE FINAL DE LA XX OLIMPIADA MATEMÁTICA PARA ALUMNOS DE 2º ESO
DE LA COMUNIDAD DE MADRID
Problemas propuestos:
Problemas individuales:
DE TODOS LOS NÚMEROS
De todos los números que cumplen que la suma de sus cifras es igual a 50 elegimos el más pequeño.
¿Cuál es su primera cifra?
¿La tercera?
¿La última?

COMPARANDO
Observa la siguiente imagen y di, razonadamente, si es mayor la superficie pintada de amarillo o la superficie pintada de rojo.
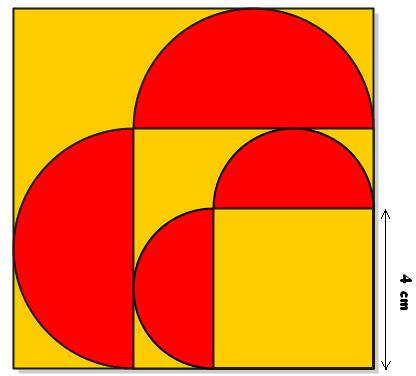
CONSERVA ECOLÓGICA
En una tienda de productos ecológicos se venden mermeladas ecológicas. Hemos pedido información sobre la elaboración de la mermelada de calabaza y Fernando, el dueño, nos ha dicho que es en la huerta murciana donde cultivan las calabazas de sus conservas.
De cada 20 kg de calabazas que recogen para hacer la mermelada, al quitarles la piel y las pipas pierden 1/4 de su peso. Lo que queda se pone a cocer con una cantidad igual de azúcar y durante la cocción la mezcla pierde 1/5 de su peso.
¿Cuántos kg de mermelada se obtienen a partir de los 20kg iniciales de calabaza?
Si quisieran obtener 30 kg de mermelada, ¿cuántos kg de calabazas necesitarían? .

Problemas en grupo:
PROTOTIPOS
La empresa Madrid Dynamics, creadora de robots dinámicos, ha creado dos prototipos: Wallace y Petman. Se ha demostrado que la movilidad por saltos de estos robots, es la más eficiente por terrenos irregulares.
Se quiere probar los dos modelos en una carrera de ida y vuelta. No podrán retroceder al punto de partida sin haber recorrido, previamente en la ida, 100 metros. Están programados de forma que:
-Wallace recorre 3m en cada salto y Petman sólo 2m en cada salto.
-Petman da 3 saltos por cada 2 saltos de Wallace.
¿Quién llegará antes al punto de partida?

LOS CUBOS
Tenemos dos cubos cilíndricos, uno blanco y otro negro. El radio del cubo blanco es el doble del radio del cubo negro, pero el nivel del agua en el cubo negro es 15 cm mayor que en el blanco. Si pasamos agua del cubo negro al cubo blanco hasta igualar los niveles, ¿cuánto aumentará el nivel del agua en el cubo blanco?

PROBLEMAS CON EL CAMBIO
Supón que solo tienes en tu cartera monedas de 1 y de 2 euros. Es bastante obvio que si quieres pagar algo que cuesta un euro, solo puedes hacerlo de una forma, esto es, dando una moneda de un euro. Para pagar algo que cuesta dos euros, sin embargo, tienes dos formas: o bien das dos monedas de un euro, o bien das una de dos euros. Sencillo, ¿verdad? Ahora bien, para pagar algo que cuesta tres euros vamos a considerar que el orden importa, es decir, que habrá tres maneras: dar una moneda de una euro y una de dos euros, o bien dar primero la de dos euros y luego la de uno (antes hemos dicho que el orden importa precisamente porque vamos a considerar estas dos formas como distintas), o, por supuesto, dar cuatro monedas de un euro (cuando las monedas son iguales el orden, claramente, es indistinguible).
Sabiendo todo esto, responde a las siguientes preguntas:
-¿De cuántas formas se podrá pagar algo que cuesta 4 euros?
-¿Y cinco euros?
-¿Ves alguna regularidad que permita enumerar las formas de pagar sin necesidad de tener que estudiar cada forma por separado? Si es así, ¿de cuántas maneras se podrá pagar algo que cuesta 10 €?

LOGOTIPO

Este logo se inscribe en un TRIANGULO DE REULEAUX de anchura constante de 8 cm. ¿Cuál es su área?
PROBLEMAS DE LA FASE SEMIFINAL XIX OLIMPIADA MATEMATICA
La fase semifinal de la XX Olimpiada Matemática para alumnos de 2º ESO de la Comunidad de Madrid tuvo lugar el jueves 22 de marzo en las diferentes sedes dispuestas para este fin.
En esta fase participaron 183 grupos pertenecientes a 68 Centros Educativos de nuestra Comunidad. Tuvieron que resolver cuatro problemas de forma individual y otros cuatro problemas en grupos mixtos de tres alumnos.
Problemas propuestos:
Problemas individuales:
LOS SOSPECHOSOS
Tenemos cuatro sospechosos de haber realizado desperfectos en clase. Preguntados sobre quién los ha provocado, responden:
María, que no usa gafas: “yo no he sido”
Jennifer, que usa gafas: “ha sido alguien que no usa gafas”
Paco, que usa gafas: “ha sido una chica”
Alberto, que no usa gafas: “ha sido alguien que usa gafas”
Tenemos la seguridad de que sólo miente uno de los cuatro y que los otros tres dicen la verdad.
¿Quién es el responsable?
CONFLICTO SABROSO
Mortadelo está muy atareado pesando varias piezas de fruta en una balanza. Después de varias pesadas, se da cuenta de que tres mandarinas y un melón pesan lo mismo que una docena de plátanos; además, advierte que el melón pesa tanto como una mandarina y ocho plátanos. Si cada plátano tiene un peso de 200 gramos, ¿cuánto crees que pesa el melón?.

ARMANDO Y DESARMANDO
Tomamos muchos cubitos de madera para formar un gran cubo macizo, de forma que cada arista de ese gran cubo está formada por seis cubitos, siendo por tanto el cubo grande de dimensiones .
A continuación pintamos la superficie exterior del cubo de color verde, pero tenemos un descuido y este se desarma, quedando todos los cubitos que lo formaban desparramados por el suelo. ¿Cuántos de esos cubitos tendrán pintadas exactamente dos de sus caras? ¿Cuántos tendrán pintada solo una cara? ¿Cuántos no estarán pintados?

SIMETRÍAS
¿Cuál es el menor número de cuadraditos que hay que sombrear en la figura para que tenga un eje de simetría?
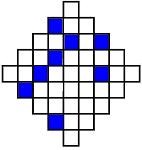
Problemas en grupo:
EL CUMPLEAÑOS
Tengo un lío horroroso con los cumpleaños de mis amigos. Un año apunté que Alfredo había celebrado su cumpleaños un viernes, Beatriz un sábado, Carmen un domingo, Jorge un miércoles y María un martes. También conozco las fechas: 8 de mayo, 21 de junio, 29 de junio, 28 de mayo, 7 de abril, pero me parece que las tengo desordenadas y no sé qué día es el cumpleaños de cada cual.
¿Seríais capaces de aclararme qué día debo felicitar a cada uno?

HACIENDO TORRES
A mi sobrino le gusta hacer torres con cubitos. Cuando empezó hacía torres de altura 3 cubitos, después consiguió hacerlas de altura 4 cubitos, más tarde de altura 5 cubitos,… Siguiendo el mismo patrón, ¿cuántos cubitos necesitará para hacer una torre de altura 10 cubitos?
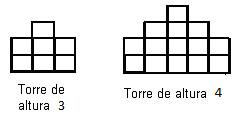
LA RANA SALTARINA (Y CAPRICHOSA)
Una rana se encuentra situada inicialmente en el origen de coordenadas de un plano. De pronto, comienza a saltar, de tal forma que sus saltos siempre son de dos tipos: o bien un salto de tres unidades en vertical y de cuatro unidades en horizontal, o bien un salto de cinco unidades en una de las direcciones, vertical u horizontal.
¿Cuál es el número mínimo de saltos que debe dar la rana para llegar al punto ?

DANDO LA VUELTA
Una escultura en forma de tetraedro (pirámide triangular regular) de 10 metros de lado se quiere rodear de un paseo de 1 metro de anchura máxima. ¿Qué área tendrá ese paseo?

RESULTADOS DE LA FASE FINAL DE LA
XX OLIMPIADA MATEMÁTICA DE LA COMUNIDAD DE MADRID
Un año más celebramos la fase final, este año de la vigésima edición, de la Olimpiada Matemáticas para alumnos de 2º ESO de la Comunidad de Madrid.
Felicitamos desde aquí a todos los participantes y más en paricular a los:
Ganadores:
| Alumno/a | Centro |
| Berta Garcia Gonzalez | IES San Juan Bautista |
| Javier Gonzalez Dominguez | IES San Juan Bautista |
| Aurora Ruiz de la Puente | IES Fortuny |
Estos alumnos serán los representantes de la Comunidad de Madrid en la Fase Nacional de la XXIII Olimpiada Matemática Nacional organizada por la Asociación del profesorado de matemáticas de Euskadi, siendo ésta una de las actividades que se engloban dentro del programa de la Federación Española de Profesores de Matemáticas.
Finalistas:
| Alumno/a | Centro |
| Diego Sánchez | Colegio Virgen Mirasierra |
| Alex Didirka Diaz | IES Luis García Berlanga |
| Daniel Puignau Chacón | IES Alameda de Osuna |
| Francisco Rodriguez Garcia | Colegio Amorós |
| Kenia Gonzalez López | IES Fortuny |
| Silvia Baquero Martinez | IES Pablo Neruda |
| Sonia Sierra Díaz | IES La Arboleda |
Durante la tarde disfrutamos de una gymkhana en la que se clasificó el grupo: “Dodecaedro”, compuesto por:
| Alumno/a | Centro |
| Alexandra Deleanu | IES Ignacio Ellacuría |
| Aurora Ruiz de la Puente | IES Fortuny |
| Daniel Prieto Rodríguez | IES Beatriz Galindo |
| Jaime Garcés | Colegio Virgen de Mirasierra |
| Javier Sanguino Bautiste | IES Ramiro de Maeztu |
| Pablo Chaure Cordero | Colegio Ntra. Sra. Del Recuerdo |
A todos los compañeros que comparten con nosotros el interés por la enseñanza y el aprendizaje de las Matemáticas a través de la resolución de problemas: ¡felicidades ! y ¡ gracias!, porque vosotros y vuestros alumnos hacéis posible esta Olimpiada. Os esperamos en la próxima edición.
ALUMNOS CLASIFICADOS PARA LA FASE FINAL DE LA XX OLIMPIADA MATEMATICA
En primer lugar damos las gracias a todos los alumnos y profesores que participaron en la fase semifinal y felicitamos a los que se han clasificado para la siguiente fase.
ALUMNOS CLASIFICADOS PARA LA FASE FINAL
DE LA XX OLIMPIADA MATEMÁTICA
| IES Alameda de Osuna | Daniel Puignau ChacónPablo Murillo CanaldaAmanda Gómez de San José |
| IES Beatriz Galindo | Daniel Prieto RodríguezPaula Zurdo BallesterosJorge Ortíz De Landazún Solans |
| IES Blas de Otero | Irene Abril CabezasPablo Medina SanzRicardo Muñóz Arnáiz |
| IES El Burgo De Las Rozas | Alberto Martínez GonzálezCelia Hermana García-AgullóIrene Rodríguez Ortega |
| IES Fortuny | Raquel Aragón GarcíaLuis Corral QueredaAurora Ruiz de la Puente |
| IES Fortuny | Alvaro García HernándezElena del Rio MolledaKenia Gonzalez López |
| IES Gabriel Cisneros | Carlos Bonillo LópezRaúl Gutiérrez TalaveraNuria Rastrero Moser-Rothschild |
| IES Ignacio Ellacuría | Jesus Alamo AlamoAlexandra DeleanuLaura De Diego Oton |
| IES La Arboleda | Ana Isabel Martín GónzalezSonia Sierra DíazVictor Cañas Villalta |
| IES Luis Garcia Berlanga | Alex Didirka DiazErnesto Gonzalez SaizNatalia Martinez Puente |
| IES Pablo Neruda | Silvia Baquero MorenoYelizaveta ArtemovaMario Bonilla Cruz |
| IES Ramiro de Maeztu | Javier Sanguino BautisteFernando Saiz GonzálezCarmen Arribas Saiz |
| IES San Juan Bautista | Berta Garcia GonzalezJavier Gonzalez DominguezPablo Ruiz Ruiz |
| Colegio Árula | Alfonso Martínez-InfanteAlonso LinaresMarta Escudero |
| Colegio Amorós | Alejandro Garcia IglesiasElena Blanco ArribasFrancisco Rodriguez Garcia |
| Colegio Salesianos Atocha | Javier Fernández del EstalLuanny Luara Caldeira MartínLaura Colastra Feliú |
| Colegio Santa María del Pilar | Manuel Rodríguez MolinaMarina Cortés CalleJuan Aguirre Lorente |
| Colegio Virgen de Mirasierra | Diego SánchezJaime GarcésLidia Valencia |
La Fase Final se celebrará el próximo sábado 26 de mayo.
La fase final consiste en un día de convivencia entre chicos y chicas de distintos lugares de la Comunidad. Por la mañana se realizarán, a partir de las 10:00h, las pruebas por equipos e individuales. Por la tarde, tras la celebración de una Gymkhana Matemática, entre las 18:00 y 18:30, tendrá lugar la entrega de premios y diplomas de participación, con asistencia libre de familiares.
Este año 2012 la Final Nacional de las Olimpiadas se celebrará del 24 al 28 de junio en Vitoria y a ella asistirán los tres ganadores de esta fase final.
