Taller de Listas y Secuencias en GeoGebra

¿Qué es una lista en GG? Es un conjunto de objetos de GG. La notación que presenta GG para las listas es {<Objeto>,<Objeto>,<Objeto>,...} aunque las listas suelen utilizarse con objetos del mismo tipo, estas admiten objetos de distintos tipos.

Ejemplo 1: lista1={(2,3),"martes", 5x^3 -2x, 2,4,7,...}

En la lista de este ejemplo hemos introducido lista1={punto, texto, función, segmento, polígono, número, ...}

Pero en la lista sólo aparece el valor del objeto:

• Si es un punto, su valor es sus coordenadas

• Si es un texto, su valor es el propio texto

• Si es una función, su valor es su ecuación

• Si es un segmento, su valor es su longitud

• Si es un polígono, su valor es su área

• Si es un número, su valor es el propio número

Lo más habitual es utilizar las listas para objetos del mismo tipo.

Ejemplo2: lista2={"lunes", "martes", "miércoles", "jueves", "viernes", "sábado", "domingo"}

Este es un ejemplo de lista de textos

Para hacer referencia a un elemento de una lista utilizaremos el comando Elemento[ ]

Ejercicio 3: Utilizaremos la lista2 del ejemplo 2

• Creamos un deslizador que llamaremos DiaSemana, que irá desde 1 hasta 7, y con un incremento de 1.

• En la barra de entrada escribimos Texto[Elemento[lista2,DiaSemana]]

Veamos ahora un ejemplos de uso de listas de números:

• Podríamos necesitar la lista de los primeros primos: {2,3,5,7,11,13,...}

• Se crean listas de números cuando usamos los comandos Divisores[ ], Múltiplos[ ],...

En CAS se usan estos mismos comandos.

Podemos utilizar las listas cuando queremos que algo sólo tome determinados valores predeterminados.

Ejemplo 4: lista4={0°, 30°, 45°, 60°, 90°}

Podríamos intentar crear una fórmula que nos generara esos números, pero las variaciones son 30, 15, 15 y 30. Resultaría más complicado.

Esta lista podría utilizarse para ver algunos ejemplos de ángulos o triángulos.

Listas de funciones. Podemos utilizar elementos aleatorios de una lista dada utilizando el comando Aleatorio[<lista>]. Esto nos puede ser muy útil para ejercicios con funciones, creando previamente una lista de funciones:

Ejemplo 5: lista5={x^2, 3x, sen(x), ...}

Aleatorio[lista5]

También podemos usar listas como un conjunto cerrado, para obligar a un elemento a pertenecer a él.

Ejemplo 6: lista6={B,C,D,E,F}

Siendo B,C,D,E,F puntos cualesquiera.

Punto[lista6] nos creará un punto que se podrá mover entre las posiciones de los puntos de la lista.

Igualmente podemos utilizar punto en lista de objetos, como por ejemplo cónicas o polígonos.

Pero sin duda el comando más potente para las listas es el comando Secuencia.

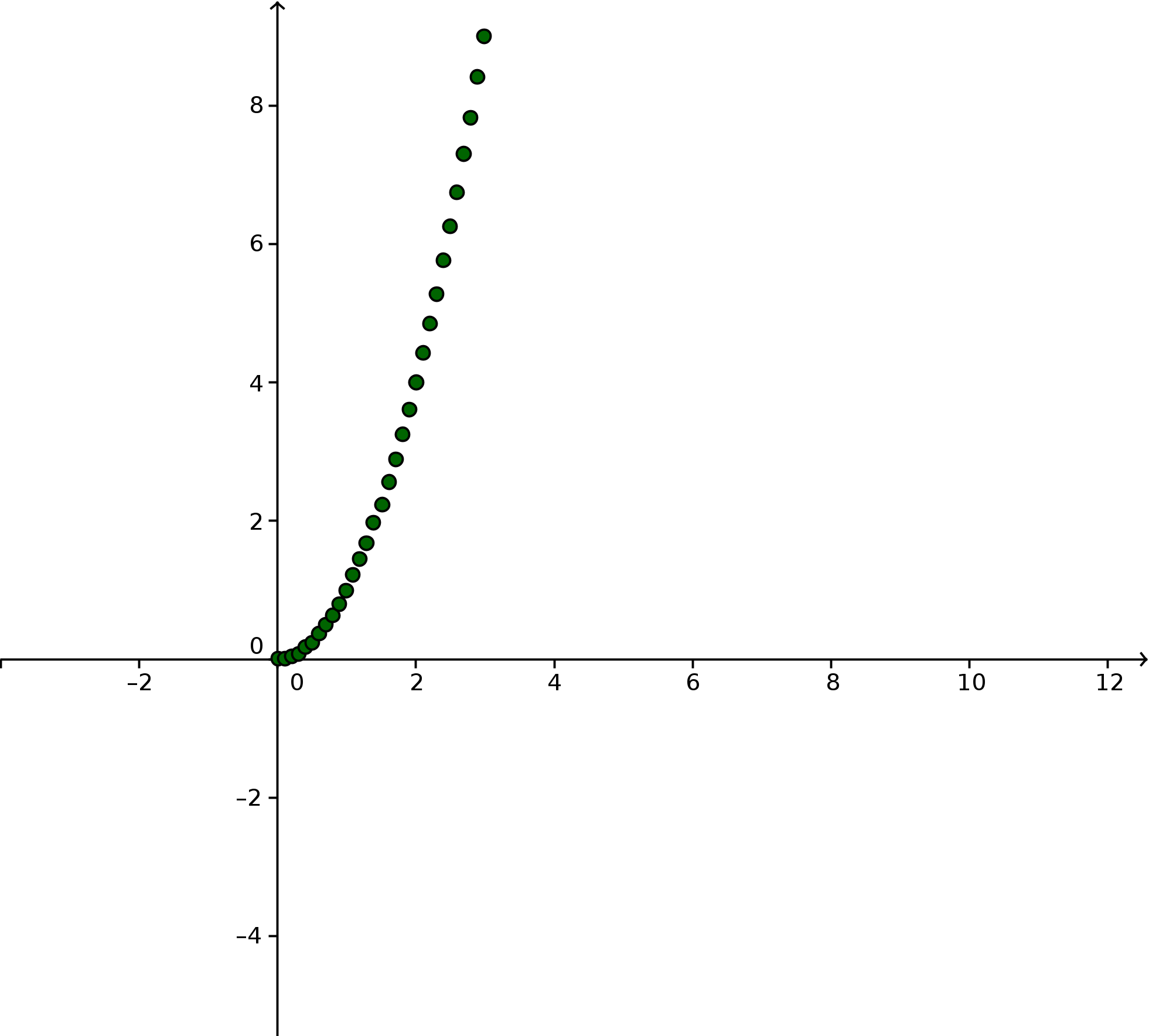
Ejemplo 7: lista7 = Secuencia[(k, k²), k, 0, 3, 0.1]

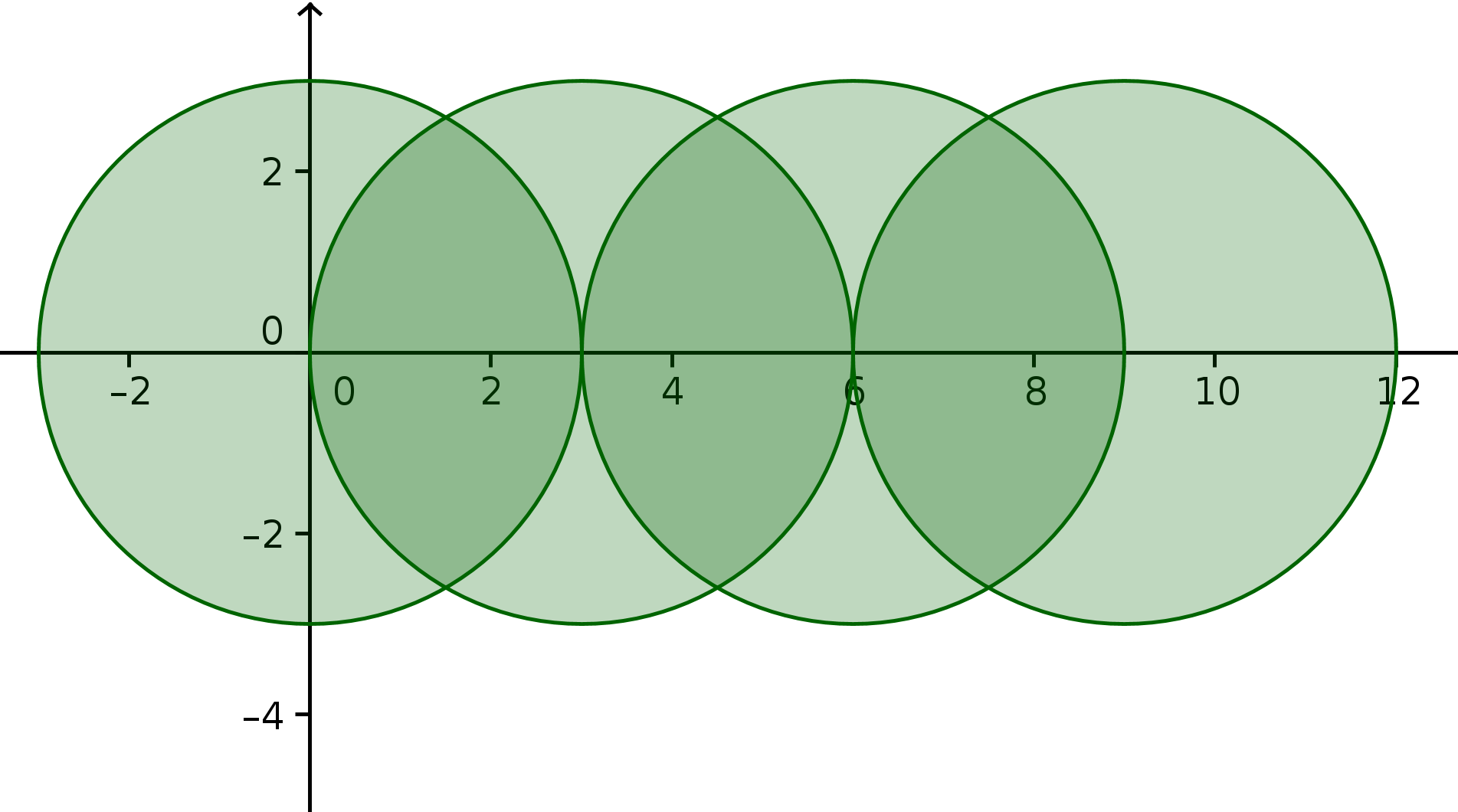
Ejemplo 8: lista8 = Secuencia[Circunferencia[(kk, 0), 3], kk, 0, 10, 3]

Ejemplo 9: lista9 = Secuencia[Circunferencia[(0, 0), k1], k1, 1, 7]

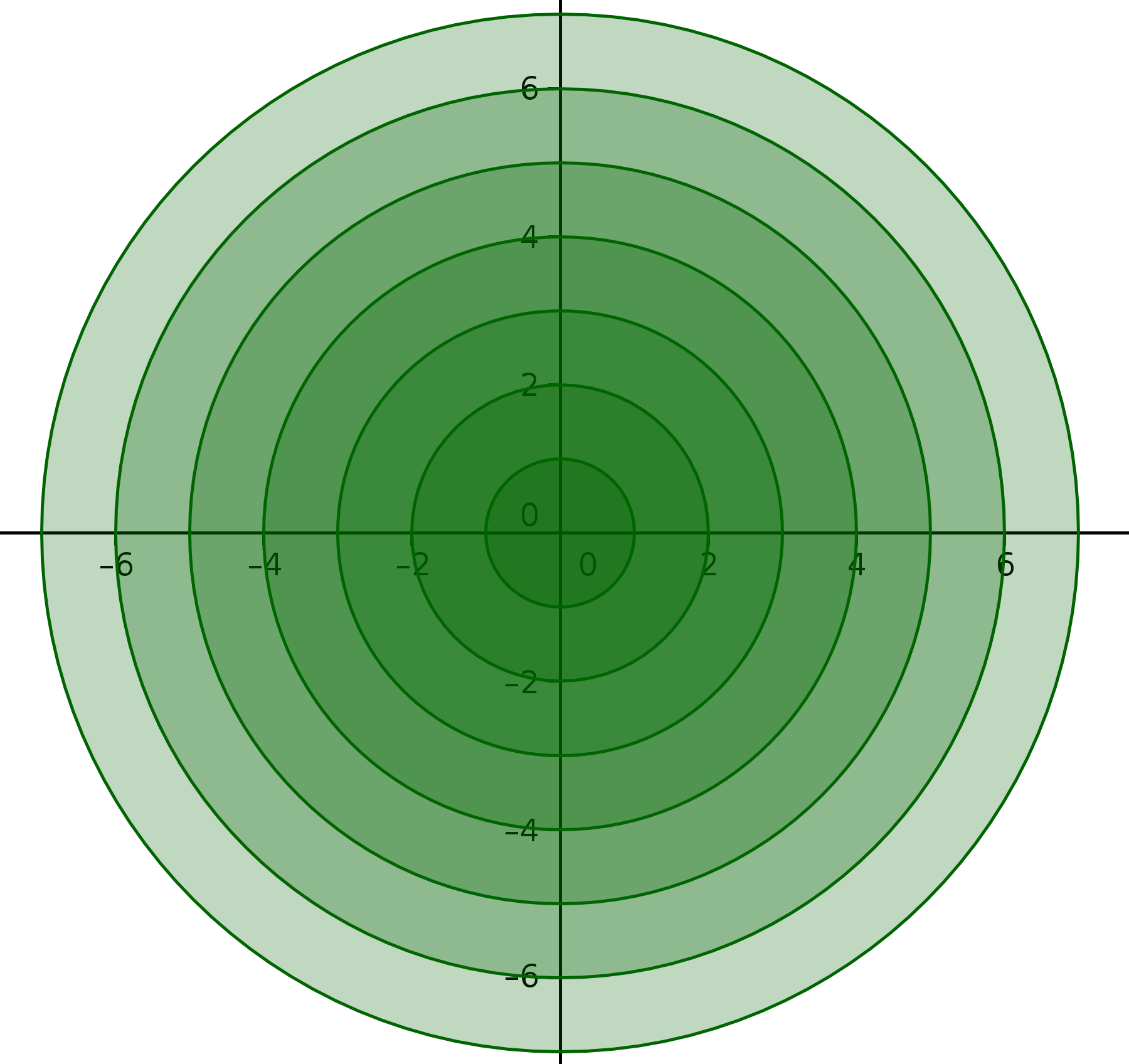
Ejemplo 10: lista10 = Secuencia[Circunferencia[(k2,0), k2], k2, 1, 7]

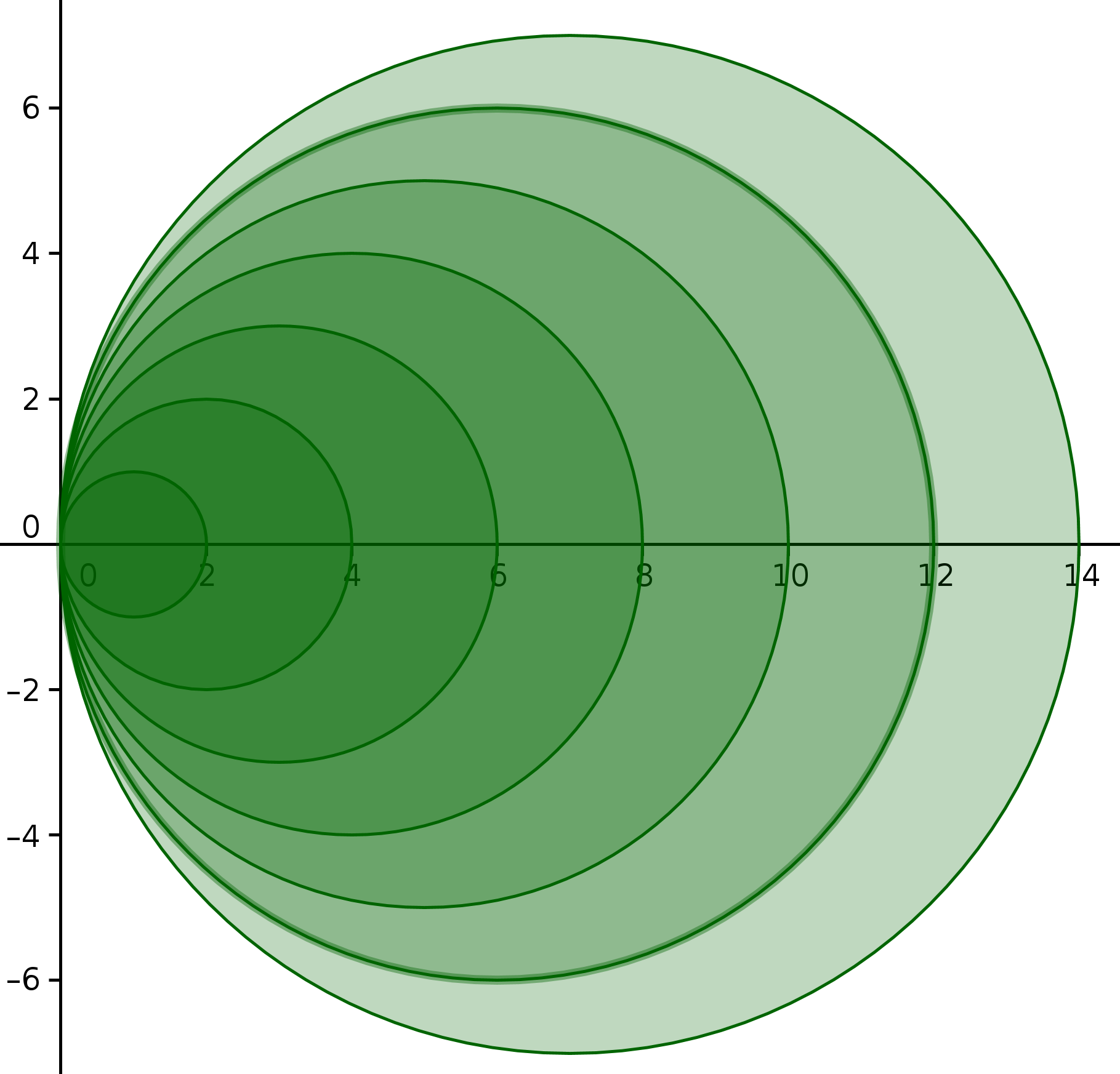
Nota:

Todos los argumentos numéricos que hemos introducido pueden ser sustituidos por variables que se pueden modificar con deslizadores, con lo que se gana en riqueza y variedad en la construcción.

Secuencias de secuencias

Aunque tiene cierta dificultad, la mayor versatilidad de las listas y secuencias se obtiene realizando listas de listas, secuencias de listas y secuencias de secuencias.

Listas de listas es lo que habitualmente se usa para matrices. Se puede introducir matrices mediante la hoja de cálculo y mediante CAS (donde podremos trabajar ampliamente con ellas)

Ejemplo 11: Secuencia[Secuencia[AleatorioEntre[1,6],k3,1,10], k4, 1, 20]

Nos generará una matriz 10x20 de valores aleatorios entre 1 y 6.

Secuencias de listas:

Ejemplo 12: Utilizando el ejemplo 4:

lista5 = Secuencia[Rota[B, Elemento[lista4, k]], k, 1, Longitud[lista4]]

lista5b = Secuencia[Polígono[A, B, Elemento[lista5, j]], j, 1, Longitud[lista5]]

Nos generará polígonos para cada ángulo de nuestra lista 4

Secuencias de Secuencias

Un ejemplo claro sería el ejemplo 11

Ejemplo 13: lista13 = Secuencia[Secuencia[Circunferencia[(k5, k6), 0.5], k5, 1, 7], k6, 1, 5]

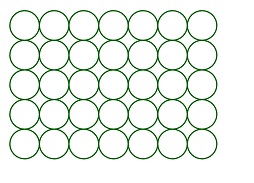
Ejercicio 2: Crear una cuadrícula 10x10

Ejercicio 3: Crear dos deslizadores m y n que variarán de 0 a 10 y con incremento 1.

lista14 = Secuencia[Secuencia[Segmento[(0, j / n), (k / m, 0)], j, 1, n], k, 1, m]

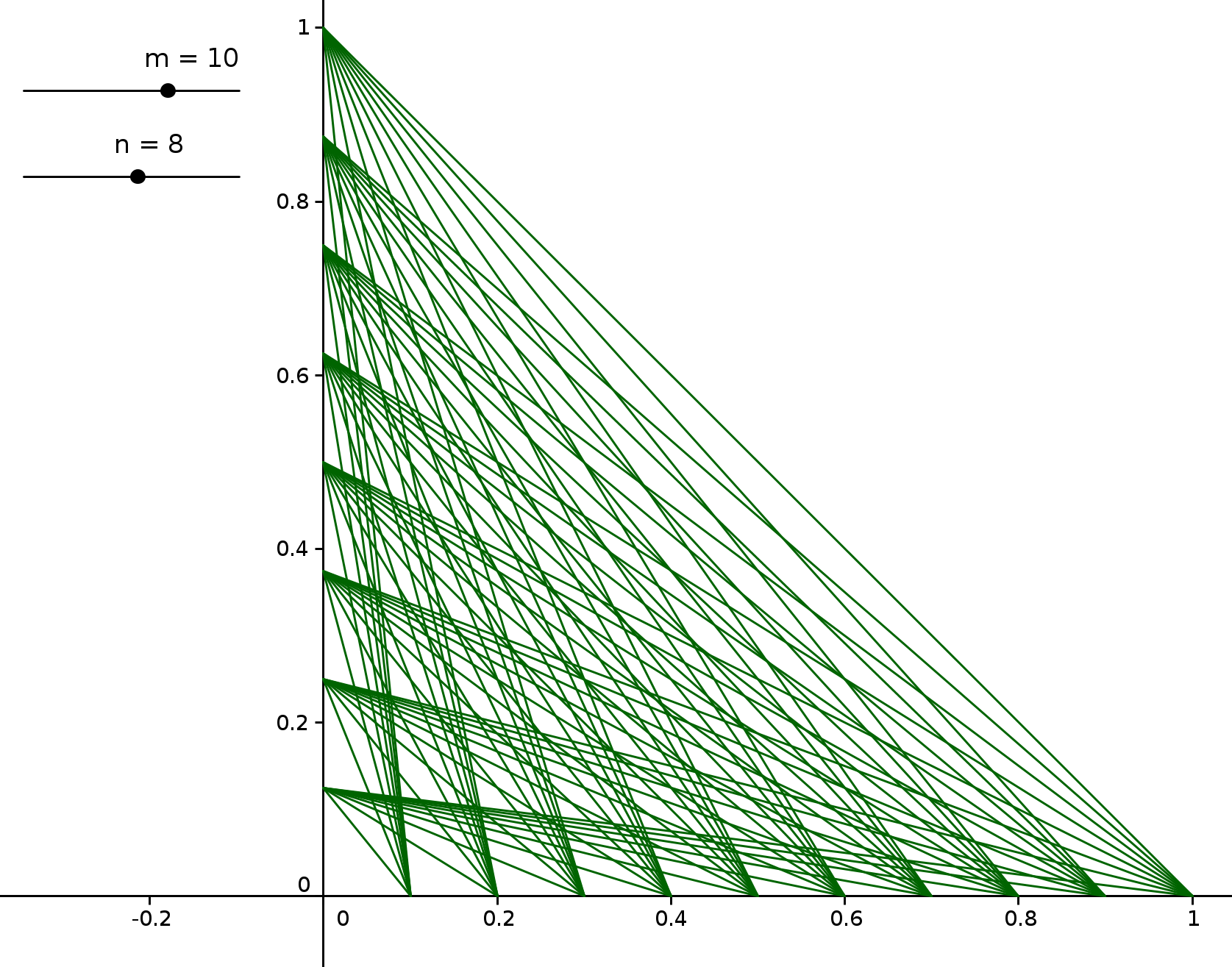
Ejercicio 4: Crear un deslizador N que variará desde 3 hasta 25, y con incremento 1.

Crear un punto A

lista15 = Secuencia[Polígono[A, Rota[A, 360° / k], k], k, 3, N]

Ejercicio 5: Crear una escalera formada por cuadrados.

lista16 = Secuencia[Secuencia[Polígono[(j, k), (j + 1, k), 4], k, 1, j], j, 1, 5]

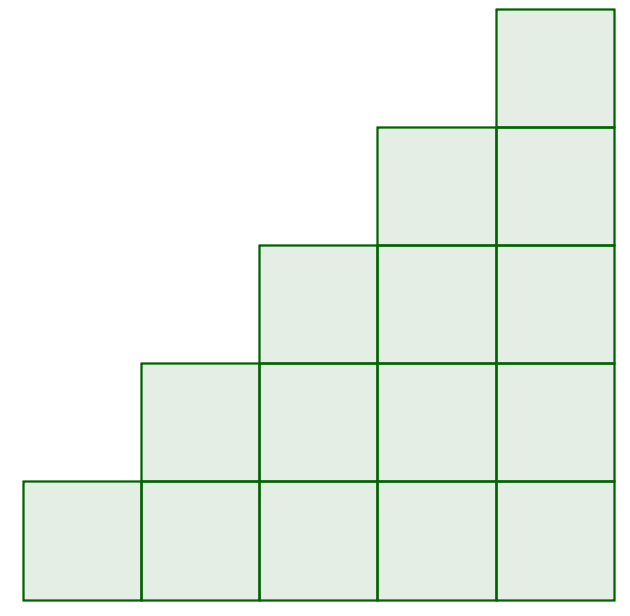
Se puede crear un deslizador N que variará desde 0 hasta 15, y con incremento 1, y en la entrada cambiar el número 5 por N, quedando así:

lista17 = Secuencia[Secuencia[Polígono[(j, k), (j + 1, k), 4], k, 1, j], j, 1, N]

Podéis encontrar algunos ejemplos en http://www.matxmat.es.

Referencias: Sequences in GeoGebra. http://ggijro.files.wordpress.com/2011/07/5francisco-maiz-jimenez-version-12bun.pdf

Es un artículo en inglés del libro GeoGebra The New Language For The Third Millennium (http://ggijro.wordpress.com/)